Jesus, All My Gladness - take 10

Take 10 is remixed with a bit less high brass, shorter holds, and more tuba. I like tuba.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness - take 9

This is the final version of the piece. I've made a few small changes to the durations of some of the long and short notes. The long half notes can now end a bit early, leaving some space in the sonority, and the short mallet instrument notes last longer.

As I said when I started this hymn, the intonation I'm using is not attempting to be historically accurate. Dear JS would roll in his grave at the heavy use of the 7/4 ratio, for example. There is no evidence that he ever considered the interval in any way useful or musical.

I chose ratios with the single goal of using the lowest possible integers in each chord. Take a look at the first phrase below, where I use two different ratios for the tenor Ab, first 8/5 in chord number 3, then 14/9 in chord number 7, 3 72-EDO steps down:

In chord numbers 8 & 9, I switch from G on 3/2 to 40/27, in order to harmonize with the D 10/9, which was forced by the chord number 7. No sane composer would have a melody haphazardly change from one version of a note to another in a melody. But when you slow everything down, it makes sense harmonically. At least to me.

I used a spreadsheet to multiply all the ratios in a chord by all the other ratios, and then minimized the integers inside the chord. See the following chart for the first ten chords. Click it to make it bigger.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness - take 8

This is a work in progress. The tuba had the wrong octave in take 6, so I removed it. I also added the ability to select a sample up or down from the one that matches the note, to allow more changes of timbre.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness - take 5

This version is more or less complete. I'll need to do some balance checks on different speakers to make sure the levels are correct.
Click to make the image bigger and see the note numbers in 72-EDO.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness - another approach

This is a work in progress. Today's version attempts to get back to some basics after wandering far afield over the past few weeks.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness - retuned & arpeggiated

This is a work in progress. Arpeggios mask the tuning. You'd hardly know it was 7-limit just.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness - retuned

Today's post is the complete hymn retuned to 7-limit just intonation, approximated by 72 EDO. I think I may have to do this again in true just, because there are some chords that beat. My goal was to have no interval in a chord beyond 7-limit, but I had to fudge a few. This is in no way a claim that Bach would have liked this. It's just an experiment in some odd harmonies. Click to enlarge the picture and see the 72-EDO notes chosen.

The next step is some transformations of using slides and trills.

Play it here: or download this link Subscribe here:

Jesus, All My Gladness

This is a work in progress.

Today's post is an arrangement of the first two lines of a hymn called Jesus, All My Gladness. It was harmonized by J.S. Bach. I can't say that I remember it from my days as a soprano in the boy choir. I sang in St. Peter's Episcopal Church in Albany, NY, from around the 3rd to the 6th grade. We must have screeched through it a time or two.

This is a very challenging tune to render in 72 EDO, 7 limit just intonation. I went through it and bent all the notes I had to to make it sound good vertically. I was merciless, and ended up with some very strange horizontal ratios, including 50/27, 40/27, and 35/27, which were necessary to keep the D at 9/10 and still have a decent minor chord. We are basically sinking down a step in 72 EDO to keep the notes sounding in tune, then just arbitrarily coming back up a step to return to the notes we started at.

The numbers in the image above in blue are the chord numbers, from 1 to 22. The numbers in green are the 72 EDO note numbers. I'll add the ratios later if I can find room. I'm still considering what to do about the chord changes. I've used 18 pitches in what would typically be rendered in 12 EDO in only 9 different pitches. I have to be able to do better than that, I would think.

Play it here: or download this link Subscribe here:

Amazing Grace - transformation #13

I generally create many versions of a piece, and then listen to find one that has something special. Today's post is the 13th pass through the algorithm, and it has a few new sounds to recommend it.

Play it here: or download this link Subscribe here:

Amazing Grace - Transformation #8

I fixed up a few erroneous sustain timings and created a few more versions. This one is take #8, and has a nice busy opening with a Conlon Nancarrow feel to it. That is, it would if Nancarrow had better access to a slide player piano with a whammy bar. The intonation is in 72 equal divisions of the octave. As before, we go through the melody seven times with different levels of variation each time. There are lots of slides from the 7:9:11 to 4:5:6, at various speeds, including slides with pitch vibrato.

I take advantage of some new envelopes I created to enable longer sustain, and even crescendos of piano notes. For example, the normal piano sound has a characteristic waveform that starts loud and gets quickly softer. Here is the waveform of a grand piano played fortissimo on a G at the bottom of the bass clef:

And here is an envlope that will attempt to smooth it out:


And the result, when Csound is told to modify the sample by the chosen envelope:


The result is a note that not only has some serious sustain, but in many cases it will actually crescendo as it sits on the note for a while. The effect is much like that of an electric guitar player using the combination of sustain and feedback to allow a note to grow as it's held.

There are many other possible envelopes that are applied at different times, resulting in sharp attacks and soft ones, depending on the choices available to each note in the piece.

Play it here: or download this linkSubscribe here:

Amazing Grace - transformed

Today's post is the first "final" version. At this stage I generate multiple passes through the algorithm looking for one that has something special. This one has some nice slides with shakes. Imagine a pair of grand pianos with bottle slides and special sustain pedals that allow the notes to resonate especially long. This version gets fast and slow. It has seven times through the melody, with various levels of alteration along the way.

Play it here: or download this linkSubscribe here:

Amazing Grace - now with a macro inside a macro

Today's post was made using a new function in my pre-processor, which reads a text file and generates Csound source code. The new function makes it possible to change the name of a macro each time it is called. For example, I've always been able to make a different macros, and call them explicitly by name:

.pian c1v67
.any01-1-a1 d12t42
&pian.&any01-1-a1.

This snippet would produce a line like this:

c1v67d12t42

Which would in turn produce a Csound score line like this:

i1 0 42 67 42

Csound would interpret each parameter as time to start, duration, loudness, pitch, etc. There are parameters for many other note characteristics, but that's enough for this example.

I can call a macro by name, or I can let the preprocessor pick one that meets a "wild card" match. For example:

.pian c1v67
.any01-1-a1 d12t42
.any01-1-a2 d12t3
&pian.&any01-1-a*.

This would either call any01-1-a1 or any01-1-a2, chosen by one randomization method or another. That was the limit to the preprocessor up until today. This meant that I would have to generate choices for all the measures in a hymn transformation. In one case, that was over 60 different sets of possible chords to choose from. The transformation of Now Thank We All Our God had over 8000 lines of source code, all done my hand. It was very tedious, and prone to error if I missed a letter or two. And if I discovered one particularly useful way to manipulate a chord near the end of my composition process, I couldn't retrofit it to all the other measures.

The new method allows me to call a macro and change which one I call using simple indirection. For example:

.pian c1v67
.any01-1-a1 d12t42
.any02-1-a1 d12t3
.num 01
&pian.&any&num.-1-a*.
.num 02
&pian.&any&num.-1-a*.

The macro name is resolved inside out: first &num. is resolved to 01, then &any01-1-a* is resolved to d12t42 or d12t3. With recursion, any number of indirections are possible. Gotta love that 1980's Turbo Pascal compiler.

This allows me to chose a different macro for each chord at execution time, but set up a massive number of variations for all chords, without coding each measure individually. That's a 60:1 savings on code size and tedium. All good.

Today's example is the first five chords of Amazing Grace, repeated seven times. The variation is set to maximum, so there are some strange slips and slides, and trills that your ordinary piano can't do. Mine can. It still sounds like a piano, just one that has some extra mechanical do-dads inside.

Play it here: or download this linkSubscribe here:

Amazing Grace - up & down

Today's post uses a Csound function table to make trills and slides. At any given time, the notes can either be played straight, trilled up to the target, from the target to the next note, slid up to the target, or down to the target note. This makes for some frantic movements at first. This is just a few measures of one chord, and there are 35 in Amazing Grace.

Here's the code for a trill up 16 steps in 72 EDO, which is a good approximation of a 7:6. The trill is 8 times up and down.
f 457 0 256 -7 1 16 1 0 1.1665290 16 1.1665290 0 1 16 1 0 1.1665290 16 1.1665290
0 1 16 1 0 1.16652904 16 1.16652904 0 1 16 1 0 1.16652904 16 1.16652904
0 1 16 1 0 1.16652904 16 1.16652904 0 1 16 1 0 1.16652904 16 1.16652904
0 1 16 1 0 1.16652904 16 1.16652904 0 1 16 1 0 1.16652904 16 1.16652904
; 7:6 156 up & down .trl7:6 g156

Graphically it looks like this:

Play it here: or download this linkSubscribe here:

Amazing Grace - slip sliding away

Today's entry has each not choosing to either slide to the next note or not, and the duration before the slide starts varies from 1/3 to 1/10th the duration of the note. For example, if I need to slide up 6 72 EDO steps, I code the following in csound:

lf 315 0 256 -6 1 218 1.0000000 12 1.0000000 12 1.0297315 12 1.0594631 1 1.0594631 1 1.0594631 ; 14 up 6 a
lf 363 0 256 -6 1 110 1.0000000 48 1.0000000 48 1.0297315 48 1.0594631 1 1.0594631 1 1.0594631 ; 14 up 6 c

This gives me one function table that rises fast, and another that's slower.
The fast one:

The slow one:

The preprocessor chooses either one, or one that doesn't slide at all.

Play it here: or download this linkSubscribe here:

Amazing Grace - sketches for a transformation

This is a work in progress. Today's sketches use my microtonal slide piano. The chords can slide from a 7:9:11 to 4:5:6, in various inversions. Csound allows for any function table to control the pitch, so I used several that are similar to this one:



The Csound code looks like this:

f 471 0 129 -6 1 4 1 4 1 16 1.0400 16 1.0801 4 1.0676 4 1.0551 4 1.0676 4 1.0801 4
1.0676 4 1.0551 4 1.0676 4 1.0801 4 1.0676 4 1.0551 4 1.0676 4 1.0801 4 1.0676 4
1.0551 4 1.0676 4 1.0801 4 1.0676 4 1.0551 4 1.0676 4 1.0801 4 1.0676 4 1.0551


The function starts at 1 and rises to 1.0801, which is 8 steps in 72 EDO, approximately a 13:12. I have a few dozen of these for the most common intervals. It falls by a single 72 EDO step and goes back up for 8 cycles or so. I think it sounds like a guitar whammy bar.

I'm not sure what this has to do with Amazing Grace, except that the first chord of the song is a G major. Just like Amazing Grace!

Play it here: or download this linkSubscribe here:

Amazing Grace - untransformed

This is a work in progress.

I have some ideas about transforming Amazing Grace, probably the most transformed hymn in the history of music. I especially like Ben Johnston's 4th string quartet, which uses the material as a jumping off point into definitely non-hymnic areas. Today's post is just a simple version of the hymn on a spinet sample.

Play it here: Or download this link
Subscribe here:

Drei Equale

This is a work in progress. I've made a few updates to the ratios of some of the notes to take the advice of some microtonalists. My ratios are shown on the JPG below in blue, Marcel de Velde's in black. I tried to eliminate the wolfs. The differences are small to Marcel's choices, a 7/6 instead of an 6/5 at chord 12 to enable the 7th overtone, and several choices that are 81/80 or 64/63 different. What's a 225/224 among friends? (chord 27: I like the 7/5, he has 43/32. I'm trying to make sure that when you hear a 3/2, it is a 3/2, and not a 20/27 or a 45/64, or something like it. That's my rule for now. See measure 5, where I've changed the 9/8's to 10/9, to keep a 3/2 instead of the 20/27.

Click to make it bigger.

Play it here: or download this link
Subscribe here:

O Sacred Head, Now Wounded - #14

For this version, I switched from 72-EDO to pure just, to hear the effect. The samples I use are as in well tuned as I can get them, but I still hear beats in some chords, even with pure just intonation. Some of the samples move around in pitch as they transition from the attack to sustain. I can imagine those poor guys in a room playing into a microphone trying to hit a pitch. There's only so much you can do with human beings, I guess.

Play it:

Subscribe here:

Drei Equale - Beethoven Trombone Quartet

This is a work in progress. Marcel de Velde has asked several microtonalists to apply our intonation efforts to retuning Ludwig Von Beethoven's Drei Equale for trombone quartet. Here's my first pass at the first 21 measures. I used Csound and a trombone sample from the McGill University Master Samples library. I don't have any midi tools available.

I've used some strange ratios, especially for the diminished triads. Measure 12 starts with a D minor, which I use 10/9 4/3 5/3. In the next chord, the A becomes an Ab to make a diminshed triad. I chose the ratio of 14/9. That makes a 5:6:7 ratio, as in the otononality scale. How else to chose? Where did the diminished triad originate?

There is another diminshed triad in measure 17, last note. I chose 6:11:13 here, and it really sticks out. Maestro LVB would not approve. Any better ideas?

Play it:

Subscribe here:

Now Thank We All Our God #9

This is a work in progress. This is the current ninth take. It's shorter than the others, at just under eight minutes. The algorithm chooses how long to stay on each chord from a list of choices, one to five beats, then repeats it zero to two times. That way, it can be as short as one beat to as long as fifteen beats on each chord.

Play it:

Subscribe here:

Now Thank We All Our God

This is a work in progress. Today's version is mostly complete. I've generated four and will pick one as the final version.

This version is another of my Transformed Hymns, which take a familiar hymn tune and stretch it out a bit. Each chord of the hymn becomes a measure or several measures of the transformation. Now Thank We All Our God is a Felix Mendelssohn harmonization of a 17th century tune. There are many unusual chord voicings in the arrangement I have, from the Center for Church Music. There are sevenths in the bass and other unusual arrangements. There are also some challenging comma issues, which I work through by switching from one note to another to preserve the harmony. My goal is to make a good just chord, and so I sacrificed melodic consistency sometimes. If a note starts out as a 16/9 to go with a 4/3, then drifts down to a 7/4 as the 7th in a major chord, it does it. No questions asked. Listen at around 1:45 in this version for the gradual 2 step in 72EDO fall in the Bb. Here it is in score form:

Here is a chart of the notes that I used in the piece. Notice how often the C, F, G, A, Bb are used, and that lonely G# passing tone as a major third to the E natural.

The piece is scored for flutes, clarinets, french horns, trombone, tuba, finger pianos, regular pianos, harp, marimba, and vibraphone.

Play it:

Subscribe here:

Nosing around some more with ratios

Nosing around further, I noticed that there was no requirement to use the Bb at ratio 16/9 in chord number 38. 7/4 is much nicer, and gets more exposure to the true 7th. I keep the G at 40/27 glides to 3/2. To clarify the tones, I switched out the horns for sine waves.

Play it:

Subscribe here:

Now Thank We All Our God - find those commas!

I'm still working my way through this one. I've found a few errors in my note choices today. At one point the score calls for a D and a G, and I used the D at ratio of 10/9 instead of the 9/8 to go with the G at 3/2. Not so nice.

At one point in chords 35 - 39 I need a G to go with the D at 10/9 and the Bb at 16/9, and with a C 1/1 E 5/4. So I chose a G 40/27 that drifts up by a step in 72 EDO to a G at 3/2 when it needs to match the C1/1. See the chart for the details. This section is heard at the end of today's excerpt. Find those commas to solve the wolf problems.

Play it:

Subscribe here:

Now Thank We All Our God - quite the crowd

This is a work in progress. Tonight, as I was enjoying my evening alone in the Salt Lake City Hilton near the airport, Omar showed up with his spinet, a blind guy who played the vibes, and a one armed marimba player. Next thing you know, the guy in the room down the hall knocked on the door. He said he could play four clarinets at once. In 72 EDO! I have never seen that before. So I had to record one more take of the first seven chords of Now Thank We All Our God. Heavenly. Fake but accurate...

Play it:

Now Thank We All Our God - loud piano

This is a work in progress. I used the FF piano samples this time. I need to figure out a way to chose the samples based on the volume.

Play it:

Subscribe here:

Now Thank We All Our God

This is a work in progress. I'm just starting up this one, for piano, harp, finger piano, brass, and flutes.

Play it:

Subscribe here:

A Mighty Fortress Is Our God - Transformed take 9

I retuned the instrument samples using a much more accurate tool (my ears). The high flute samples were out of tune before. Now they sound much better. I also fixed a bug in the hold values for the flute part in the last section, so that they don't get chopped off early. This version should be the last one posted.

Play it:

Subscribe here:

A Mighty Fortress Is Our God - Transformed take 5

This version is much tighter now, and I think it's finished. The hymn tune was written by Martin Luther in 1529, and harmonized by Bach in 1740 or so. This version stretches each chord in a variety of ways. Each chord can be 2, 3, 4, or 5 times longer than normal, and is repeated 1, 2, or 3 times before moving on to the next chord. There is a variable repetition scheme that includes stepping through the choices of arpeggios in sequence, forward and backward, and staying put for a while. The tempo shifts constantly, as does the volume.

The intonation system is chosen from the 72 EDO scale. The notes include the following: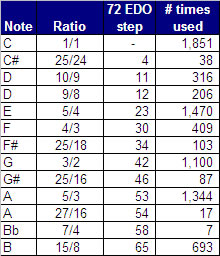

Notice how many more times C, E, G, and A are played. The two D's are less than half as common, and that lonely 7/4 is only played 7 times. See if you can hear it, towards the end.

This version is scored for vibraphone, marimba, finger piano, tuba, trombone, French horn, and flutes.

Here is a link to a nice PDF of the file on the Center for Church Music site. It's not the one I used, but it's close.

Play it:

Subscribe here:

A Mighty Fortress Is Our God - Transformed

This is a work in progress. It's a bit long now. I'll have to figure out a way to shorten it up a bit.

Play it:

Subscribe here: